Historias Matemáticas

HISTORIA DE LA GEOMETRÍA

GEOMETRÍA (Del griego geo "tierra" metrein "medir") rama de las matemáticas que se preocupa de las propiedades del espacio. En su forma más elemental, la geometría se preocupa de problemas métricos como el cálculo del área y diámetro de figuras planas y de la superficie y volúmenes de cuerpos sólidos. Otros campos de la geometría son la geometría de espacio con cuatro o más dimensiones, geometría fractal y geometría no euclidiana.

GEOMETRÍA DEMOSTRATIVA PRIMITIVA

El origen del término geometría es una descripción precisa del trabajo de los primeros geómetras que se preocupaban de la medida de los tamaños de los campos o el trazado de ángulos rectos para edificios. Este tipo de geometría empírica que floreció en el antiguo Egipto, Sumeria, y Babilonia, fue refinado y sistematizado por los griegos. En el siglo VI a.c. El matemático Pitágoras colocó la piedra angular de la geometría científicas al demostrar que las diversas leyes arbitrarias e inconexas de la geometría empírica se puede deducir como conclusiones lógicas de un número limitado de axiomas o postulados.
MODERNOS AVANCES

La geometría sufrió un cambio radical de dirección en el siglo XIX, los matemáticos Carl Friedrich Gauss, Nikolai Lobachevski y János Bolyai trabajando por separado, desarrollaron sistemas coherentes de geometría no euclidiana. Estos sistemas aparecieron a partir de los trabajos sobre el llamado "Postulados Paralelos" de Euclides. Se desarrolló la geometría para espacios con más de tres dimensiones. Imaginemos que una línea es un espacio unidimensional. Si cada uno de los puntos de la línea se sustituye por una línea perpendicular a ella, se crea un plano, se sustituye por una línea perpendicular a él, se genera un espacio tridimensional.

PRIMEROS PROBLEMAS GEOMÉTRICOS

Los griegos introdujeron los problemas de construcción, en los que cierta línea o figura debe ser construida utilizando sólo una regla de borde recto y un compás. Hay tres famosos problemas de construcción que data de la época griega se resistieron al esfuerzo de muchas generaciones de matemáticos que intentaron resolverlos:

* La duplicación del cubo.

* La cuadratura del círculo.

* Trisección del ángulo.

Ninguna de estas construcciones es posible de realizarlo con compás y la imposibilidad de la cuadratura del circulo no fue finalmente demostrada hasta 1882.

APORTES DE LA GEOMETRIA A LA HUMANIDAD

“La geometría es una rama de las matemáticas que estudia idealizaciones del espacio, como son: puntos, rectas, planos, polígonos, poliedros, curvas, superficies, etc. Se utiliza para solucionar problemas concretos y es la justificación teórica de muchos instrumentos, por ejemplo el compás, el teodolito y el pantógrafo”.[1]

Los orígenes de la geometría se remontan a los principios de la humanidad, pues, quizá, el hombre primitivo clasificaba inconscientemente los objetos que lo rodeaban según su forma, realizando abstracciones que lo acercaban de manera intuitiva a la geometría.

La geometría griega fue la primera en ser formal; al respecto se destacan personajes importantes como:
- Tales de Mileto, quien a través del cono cimiento geométrico, según la historia, fue capas de predecir un eclipse solar.
- Pitágoras: eleva el concepto de número a categoría de elemento primigenio y asienta definitivamente el concepto de demostración.
- Eratóstenes: medición del radio de la tierra y la distancia a la luna.
- Euclides: quizá uno de los personajes más importantes de la geometría; escribe el libro LOS ELEMENTOS, donde plantea el modelo de sistema axiomático – deductivo.
Posteriormente, con el renacimiento la geometría surge una gran transformación de la que son participe importantes matemáticos tales como: Luca Pacioli, Desargues, Pascal, Poncelet, entre otros. Sin embargo, son Rene Descartes y Pierre de Fermat quienes dan el paso definitivo a lo que se conoce hoy como Geometría Analítica. Lo novedoso es que ésta permite representar figuras geométricas mediante fórmulas del tipo f(x,y) = 0, donde f representa una función.

Cabe hacer mención también del aporte contemporáneo de Gauss quien introduce el estudio de Variable Compleja y crea lo que se denomina actualmente con Geometría Diferencial.

En cuanto a la aplicabilidad de la geometría, vale la pena complementar diciendo que ésta da fundamento teórico a inventos como el sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales) y es útil en la preparación de diseños (justificación teórica de la geometría descriptiva, del dibujo técnico e incluso en la fabricación de artesanías). Resáltese que éstas son solo unas pocas de las tantas aplicaciones de la geometría, por tanto, la invitación es investigar al respecto y dejar correr la imaginación en función de profundizar en tan magníficos saberes.

FIGURAS GEOMETRICAS

SISTEMAS DE NUMERACIÓN
Los sistemas de numeración son las distintas formas de representar la información numérica. Se nombran haciendo referencia a la base, que representa el número de dígitos diferentes para representar todos los números.

El sistema habitual de numeración para las personas es el Decimal, cuya base es diez y corresponde a los distintos dedos de la mano, mientras que el método habitualmente utilizado por los sistemas electrónicos digitales es el Binario, que utiliza únicamente dos cifras para representar la información: el 0 y el 1.

Otros sistemas como el Octal (base y el Hexadecimal (base 16) son utilizados en las computadoras.

NUMERACIÓN DECIMAL Y BINARIA

Cuando en una numeración se usan diez símbolos diversos, a ésta se la denomina numeración decimal o en base 10. El valor de cada cifra es el producto de la misma por una potencia a 10 (la base), cuyo exponente es igual a la posición 0, las decenas la 1 y así sucesivamente.

Por ejemplo, 327 se puede descomponer en:

3 . 10² + 2 . 10¹ + 7 . 10º = 300 + 20 + 7 = 327

Siguiendo con el mismo razonamiento, podemos definir una numeración binaria o en base 2, donde los símbolos 0 y 1 vistos anteriormente asumen el valor numérico 0 y 1. Así, el número 10110 escrito en base 2 o binaria equivale al siguiente número en base 10 o decimal:

1 . 24 + 0 . 2³ + 1 . 2² + 1 . 2¹ + 0 . 2º = 16 + 0 + 4 + 2 + 0 = (22)10

En el sistema binario:

- Con 1 bit el valor más alto que se puede expresar es el 1.

- Con 2 bits el valor más alto que se puede expresar es el 3.

- Con n bits el valor más alto que se puede expresar es el 2 – 1.

Cada bit, según la posición que ocupa dentro del conjunto de un número binario, tiene un peso o un valor determinado en el sistema decimal.

Como vemos, el sistema binario emplea muchas cifras para representar una información. Para poder trabajar con más comodidad, los programadores emplean los sistemas octal y hexadecimal, que permiten operar con muchas menos cifras.

SISTEMA NUMÉRICO BINARIO

Los circuitos digitales internos que componen las computadoras utilizan el sistema de numeración Binario para la interpretación de la información y codificación de la misma.

El sistema decimal de numeración que usamos en la vida diaria es de difícil empleo en las computadoras, ya que para representar los números y trabajar con ellos son necesarios diez símbolos: 0 1 2 3 4 5 6 7 8 9
Los circuitos de una computadora que trabajara con el sistema decimal deberían ser capaces de distinguir entre diez valores o posiciones de funcionamiento distintas. Esto exigiría una precisión difícil de conseguir, por lo que se ha elegido un sistema de numeración que simplifica mucho el diseño de los circuitos, porque exige sólo dos estados o posiciones de funcionamiento.

El sistema binario utiliza sólo dos signos: 0 1

Estos son mucho más fáciles de representar en el interior de una computadora, donde estas dos cifras se pueden asociar perfectamente a los dos posibles estados que pueden adoptar los circuitos o componentes electrónicos: apagado y encendido. La presencia de una corriente eléctrica = 1 (encendido) y la ausencia = 0 (apagado). Cuando la corriente eléctrica pasa a través de la computadora, ésta lee un 1 cuando percibe la corriente eléctrica y un 0 cuando no hay corriente eléctrica.
A las cifras o símbolos binarios les denominaremos, por convención, bits.

bit cero = 0

bit uno = 1

La palabra «bit» es una contracción de las palabras inglesas binary digit, dígito binario.

El bit es la unidad más pequeña de información. Aislado, nos permite distinguir sólo entre dos posibilidades: sí-no, blanco-negro, abierto-cerrado, positivo-negativo. Permite sólo dar dos respuestas a una pregunta, sin matices.

La combinación de estos dos símbolos un determinado número de veces permite la codificación de toda la información posible. Si codificamos una serie de bits dándole a cada uno un significado según nuestro deseo, el cojunto de bits representa un conjunto de información.

Por consiguiente, si sustituimos el valor dado a cada bit por otro, tendremos que una misma combinación de bits queda modificada en cuanto al significado:

- Con un solo bit, se representan dos informaciones o estados (2¹).

- Con dos bits (2²), obtenemos cuatro combinaciones de información.

- Con tres bits (2³), ocho combinaciones de información.

- Con cuatro bits (24), dieciséis combinaciones de información.

- Con n bits, (2n) combinaciones de información.

Si deseamos representar cada letra del alfabeto mediante una combinación de bits, necesitamos que cada letra esté representada por lo menos por 5 bits (25 = 32). Si, además, deseamos abarcar todos los signos gráficos y las letras, tanto minúsculas como mayúsculas, necesitaremos una combinación de 7 bits (27 = 128).

TRANSFORMACIÓN DE DECIMAL A BINARIO

Para cambiar un número decimal a número binario, se divide el número entre dos. Se escribe el cociente y el residuo. Si el cociente es mayor que uno, se divide el cociente entre dos. Se vuelve a escribir el cociente y el residuo. Este proceso se sigue realizando hasta que el cociente sea uno. Cuando el cociente es uno, se escribe el cociente y el residuo. Para obtener el número binario, una vez llegados al 1 indivisible, se cuentan el último cociente, es decir el uno final (todo número binario excepto el 0 empieza por uno), seguido de los residuos de las divisiones subsiguientes. Del más reciente hasta el primero que resultó. Este número será el binario que buscamos. A continuación analizaremos dos ejemplos de números decimales transformados al sistema binario:

NÚMERO DECIMAL 26 TRANSFORMADO AL SISTEMA BINARIO

NÚMERO DECIMAL 8 TRANSFORMADO AL SISTEMA BINARIO

Recordemos que se comienza a contar desde el cociente 1 hasta el primer residuo que nos resultó. Sin embargo, existe otra manera de hacerlo y es dividir el cociente 1 entre 2, escribimos 0 como cociente, posteriormente multiplicamos 2 por 0 (que es cero) y ese resultado se lo restamos al último residuo que teníamos (que será 1) y tendremos como residuo 1. De esta forma comenzaremos la cuenta para obtener el valor binario desde el último residuo obtenido (que es siempre 1, excepto en el caso del número 0) hasta el primero. Podemos utilizar cualquiera de los dos métodos y ambos son correctos y presentan el último resultado, tal como veremos en los ejemplos a continuación.

Ahora veremos tres nuevos ejemplos de transformación de un número del sistema decimal al sistema binario:

TABLA POSICIONAL DE LOS NUMEROS DECIMALES

PARTE ENTERA
Millón-Centena de millar-Decena de millar-Unidad de millar-Centenas-Decenas- Unidad
COMA DECIMAL (,)
Décimos-Centésimos-Milésimos-Diezmilésimos-Cienmilésimos-Millonésimos-Diezmillonésimos-Cienmillonésimos-Milmillonésimos-Diez mil millonésimos-Cien mil millonésimos-Billonésimos-..........
PARTE DECIMAL

Con estos datos resuelve tu tarea.Buena suerte alumno xammarino

HISTORIA DEL CERO

Una de las preguntas más comunes que los lectores de este archivo hacen es: ¿Quién descubrió el cero? ¿Por qué entonces no hemos escribo un artículo como este en los inicios del archivo? La razón es, básicamente, debido a la dificultad de contestar a la pregunta de una forma satisfactoria. Si alguien tuvo por primera vez la idea del cero, la cual todo el mundo vio como una brillante innovación a introducir en las matemáticas a partir de ese momento, la pregunta tendría una respuesta satisfactoria incluso si no conociésemos el genio que lo inventó. Los registros históricos, sin embargo, muestran unas vías bastante distintas hacia dicho concepto. El cero hace apariciones fantasmales solo para desvanecerse de nuevo casi como si un matemático estuviese buscándolo pero no reconociese su significado fundamental incluso aún viéndolo.

Lo primero que hay que decir sobre el cero es que hay dos usos para el cero, ambos extremadamente importantes, pero algo distintos. Un uso es como indicador de lugar vacío en nuestro sistema numérico de valor por posición. Así pues, en un número como 2106, el cero es usado para que las posiciones del 2 y del 1 sean correctas. Claramente 216 significa algo bastante distinto. El segundo uso del cero es como un número en sí mismo, en la forma que lo usamos como 0. Hay también otros aspectos distintos del cero en estos dos usos, a saber, el concepto, la notación y el nombre. (Nuestro nombre “cero” deriva del árabe sifr el cual también nos da la palabra 'cifra'.)

Ninguno de los usos de arriba tienen una fácil descripción histórica. No sucedió que alguien inventó las ideas y entonces todo el mundo comenzó a usarlos. También es justo decir que el número cero está lejos de ser un concepto intuitivo. Los problemas matemáticos comenzaron como problemas “reales” más que como problemas abstractos. Los números en los primeros momentos de la historia eran concebidos de una forma mucho más concreta que los abstractos conceptos que son nuestros números de hoy. Hay un salto mental gigantesco de 5 caballos a 5 “cosas” y de ahí a la idea abstracta de “cinco”. Si los antiguos resolvían un problema sobre cuántos caballos necesitaba un granjero el problema no iba a tener un resultado de 0 o -23 como respuesta.

Se podría pensar que una vez que aparece un sistema numérico de valor por posición entonces el 0 como indicador de posición vacía es una idea necesaria, aunque los babilonios tuvieron un sistema numérico de valor por posición sin esta característica durante 1000 años. Además no hay ninguna evidencia de que los babilonios sintiesen que había algún problema con la ambigüedad que existía. Extraordinariamente, sobrevivieron textos originales de la época de los matemáticos babilonios. Los babilonios escribían en tablas de arcilla sin cocer, usando escritura cuneiforme. Los símbolos se escribían en las tablas de arcilla blanda con el afilado ángulo de una aguja y por esto tienen una forma de cuña (de aquí el nombre de cuneiforme). Sobreviven muchas tablas de alrededor del año 1700 a. C. y podemos leer los textos originales. Por supuesto su notación numérica era bastante distinta de la nuestra (y no en base 10 sino en base 60) pero la traducción a nuestro sistema de notación no distinguiría entre el 2106 y el 216 (el contexto tendría que mostrar a qué nos referimos). No fue hasta alrededor del 400 a. C. que los babilonios colocaron dos símbolos de cuña en el lugar dónde pondríamos nuestro cero para indicar si significa 216 o 21”6.

HISTORIA DE LOS NUMEROS REALES

Los egipcios utilizaron por primera vez las fracciones comunes alrededor del año 1000 a. C.; alrededor del 500 a. C. el grupo de matemáticos griegos liderados por Pitágoras se dio cuenta de la necesidad de los números irracionales. Los números negativos fueron ideados por matemáticos indios cerca del 600, posiblemente reinventados en China poco después, pero no se utilizaron en Europa hasta el siglo XVII, si bien a finales del XVIII Leonhard Euler descartó las soluciones negativas de las ecuaciones porque las consideraba irreales. En ese siglo, en el cálculo se utilizaba un conjunto de números reales sin una definición concisa, cosa que finalmente sucedió con la definición rigurosa hecha por Georg Cantor en 1871.

En realidad, el estudio riguroso de la construcción total de los números reales exige tener amplios antecedentes de teoría de conjuntos y lógica matemática. Fue lograda la construcción y sistematización de los números reales en el siglo XIX por dos grandes matemáticos europeos utilizando vías distintas: la teoría de conjuntos de Georg Cantor (encajamientos sucesivos, cardinales finitos e infinitos), por un lado, y el análisis matemático de Richard Dedekind (vecindades, entornos y cortaduras de Dedekind). Ambos matemáticos lograron la sistematización de los números reales en la historia, no de manera espontánea, sino utilizando todos los avances previos en la materia: desde la antigua Grecia y pasando por matemáticos como Descartes, Newton, Leibniz, Euler, Lagrange, Gauss, Riemann, Cauchy y Weierstrass, por mencionar sólo a los más sobresalientes.

Tipos de números reales
Un número real puede ser un número racional o un número irracional. Los números racionales son aquellos que pueden expresarse como el cociente de dos números enteros, tal como 3/4, -21/3, 5, 0, 1/2, mientras que los irracionales son todos los demaś. Los números racionales también pueden describirse como aquellos cuya representación decimal es eventualmente periódica, mientras que los irracionales tienen una expansión decimal aperiódica:

Ejemplos: 1/4 = 0.250000... ES un número racional puesto que es periódico a partir del tercer numero decimal.; 5/7 = 0.7142857142857142857.... ES racional y tiene un período de longitud 6 (repite 714285).; $frac{sqrt[3]{7}+1}{2}=1.456465591386194ldots$ es irracional y su expansión decimal es aperiódica

Otra forma de clasificar los números reales es en algebraicos y trascendentes. Un número es algebraico si existe un polinomio que lo tiene por raíz y es trascendente en caso contrario. Obviamente, todos los números racionales son algebraicos: si $frac{p}{q}$ es un número racional, con p entero y q natural, entonces es raíz del binomio qx=p. Sin embargo, no se cumple el recíproco, no todos los números algebraicos son racionales.

Ejemplos

El número $frac{sqrt[3]{7}+1}{2}$ es algebraico puesto que es la raíz del polinomio

8 x 3 - 12 x 2 + 6 x - 8

Un ejemplo de número trascendente es $ln(3)=1.09861228866811ldots$
Operaciones con números reales

Con números reales pueden realizarse todo tipo de operaciones básicas con dos excepciones importantes:

No existen raíces de orden par (cuadradas, cuartas, sextas, etc.) de números negativos en números reales, razón por la que existe el conjunto de los números complejos donde estas operaciones sí están definidas.
No existe la división entre cero, pues carece de sentido dividir entre nada o entre nadie, es decir, no existe la operación de dividir entre nada.

Estas dos restricciones tienen repercusiones importantes en ramas más avanzadas de las matemáticas: existen asíntotas verticales en los lugares donde una función se indefine, es decir, en aquellos valores de la variable en los que se presenta una división entre cero, o no existe gráfica real en aquellos valores de la variable en que resulten números negativos para raíces de orden par, por mencionar un ejemplo de construcción de gráficas en geometría analítica.

La principal característica del conjunto de los números reales es la completitud, es decir, la existencia de límite para dada sucesión de Cauchy de números reales.

Notación

Los números reales miden cantidades continuas que se expresan con fracciones decimales que tienen una secuencia infinita de dígitos a la derecha de la coma decimal, como por ejemplo 324,8232. Frecuentemente también se subrepresentan con tres puntos consecutivos al final (324,823211247…), lo que significaría que aún faltan más dígitos decimales, pero que se consideran sin importancia.

Las medidas en las ciencias físicas son siempre una aproximación a un número real. No sólo es más conciso escribirlos con forma de fracción decimal (es decir, números racionales que pueden ser escritos como proporciones, con un denominador exacto) sino que, en cualquier caso, cunde íntegramente el concepto y significado del número real. En el análisis matemático los números reales son objeto principal de estudio. Puede decirse que los números reales son la herramienta de trabajo de las matemáticas de la continuidad, como el cálculo y el análisis matemático, mientras que los números enteros lo son de las matemáticas discretas, en las que está ausente la continuidad.

Se dice que un número real es recursivo si sus dígitos se pueden expresar por un algoritmo recursivo. Un número no-recursivo es aquél que es imposible de especificar explícitamente. Aun así, la escuela rusa de constructivismo supone que todos los números reales son recursivos.

Los ordenadores sólo pueden aproximarse a los números reales por números racionales; de todas maneras, algunos programas de ordenador pueden tratar un número real de manera exacta usando su definición algebraica (por ejemplo, " $sqrt{2}$ ") en vez de su respectiva aproximación decimal.

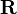Los matemáticos usan el símbolo $mathbb R$ (o, de otra forma, $mathbf{R}$ , la letra "R" en negrita) para representar el conjunto de todos los números reales.

La notación matemática 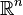$mathbb R^n$ se refiere a un espacio de $n$ dimensiones de los números reales; por ejemplo, un valor $mathbb R^3$ consiste de tres números reales y determina un lugar en un espacio de tres dimensiones.

En matemática, la palabra "real" se usa como adjetivo, con el significado de que el campo subyacente es el campo de los números reales. Por ejemplo, matriz real, polinomio real, y Álgebra de Lie real.

APORTES DE EUCLIDES A LA MATEMATICA

Su obra Los elementos, es una de las obras científicas más conocidas del mundo y era una recopilación del conocimiento impartido en el centro académico. En ella se presenta de manera formal, partiendo únicamente de cinco postulados, el estudio de las propiedades de líneas y planos, círculos y esferas, triángulos y conos, etc.; es decir, de las formas regulares. Probablemente ninguno de los resultados de "Los elementos" haya sido demostrado por primera vez por Euclides pero la organización del material y su exposición, sin duda alguna se deben a él. De hecho hay mucha evidencia de que Euclides usó libros de texto anteriores cuando escribía los elementos ya que presenta un gran número de definiciones que no son usadas, tales como la de un oblongo, un rombo y un romboide. Los teoremas de Euclides son los que generalmente se aprenden en la escuela moderna. Por citar algunos de los más conocidos:

La suma de los ángulos interiores de cualquier triángulo es 180°.
En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, que es el famoso teorema de Pitágoras.

En los libros VII, VIII y IX de los Elementos se estudia la teoría de la divisibilidad.

APORTES DE TARTAGLIA A LA MATEMATICA

Descubridor de un método para resolver ecuaciones de tercer grado, estando ya en Venecia, en 1535 su colega del Fiore discípulo de Scipione del Ferro de quien había recibido la formula para resolver las ecuaciones cúbicas, le propone un duelo matemático que Tartaglia acepta. A partir de este duelo y en su afán de ganarlo Tartaglia desarrolla la fórmula general para resolver las ecuaciones de tercer grado. Por lo que, consigue resolver todas las cuestiones que le plantea su contrincante, sin que éste logre resolver ninguna de las propuestas por Tartaglia.

El éxito de Tartaglia en el duelo llega a oídos de Gerolamo Cardano que le ruega que le comunique su fórmula, a lo que accede pero exigiéndole a Cardano jurar que no la publicará. Sin embargo, en vista de que Tarataglia no publica su fórmula, y que según parece llega a manos de Cardano un escrito inédito de otro matemático fechado con anterioridad al de Tartaglia y en el que independiente se llega al mismo resultado, será finalmente Cardano quien, considerándose libre del juramento, la publique en su obra Ars Magna (1570). A pesar de que Cardano acreditó la autoría de Tartaglia, éste quedó profundamente afectado, llegando a insultar públicamente a Cardano tanto personal como profesionalmente. Las fórmulas de Tartaglia serán conocidas como fórmulas de Cardano

Otras aportaciones destacables de Tartaglia fueron los primeros estudios de aplicación de las matemáticas a la artillería en el cálculo de la trayectorias de los proyectiles (trabajos confirmados posteriormente por los estudios acerca de la caída de los cuerpos realizados por Galileo), así como por la expresión matemática para el cálculo del volumen de un tetraedro cualquiera en función de las longitudes de sus lados, la llamada fórmula de Tartaglia, una generalización de la fórmula de Herón (usada para el cálculo del área del triángulo):

Además de sus trabajos matemáticos, Tartaglia publicó las primeras traducciones al italiano de las obras de Arquímedes y Euclides.

APORTES DE FERRARI A LA MATEMATICA
Los aportes de Ferrari
Algunos años después, Cardano descubrió el método para reducir una ecuación arbitraria de tercer grado a una del tipo de la de arriba. Descubrió también que en el caso irreductible del llamado discriminante era un número menor de cero, la ecuación tiene tres raíces distintas.
Hacia la misma época, Ferrari, un alumno de Cardano, resolvió la ecuación de cuarto grado. Para los matemáticos crecieron las esperanzas de que se podría resolver una ecuación algebraica de grado arbitrario. No obstante, las investigaciones en el sentido de adelantar la solución para la ecuación de quinto grado peregrinaron sin éxito por más de tres siglos.

APORTES DE GEORGE CANTOR
Sus principales aportes estan referidos al desarrollo de una
teoría de los números irracionales, a una peculiar matematica
del infinito y a la de conjuntos sobre la que se basa la
matemática moderna. Su teoria sobre la matematicas del
infinito presentada alrededor de 1872 suscito no pocas resistencias
en su epoca entre colegas, no habiendo podido ser aun
demostrada .Georg Cantor y su teoría sobre los conjuntos infinitos irrumpe sobre el final del mismo siglo y se prolonga hasta principios del siglo pasado, creando en algún sentido un paraíso para la investigación en matemática. Cantor terminó poco menos que
“loco” y vilipendiado por una comunidad que no lo comprendió.

APORTES DE R. DEDEKIND

Aunque Dedekind ha publicado algunas memorias interesantes acerca de las ecuaciones binomias, de las funciones modulares y abelianas, y algunos otros asuntos diversos, sus trabajos fundamentales versan sobre la teoría de números enteros, especialmente los enteros algébricos, teorías en las que ha introducido las nociones de cortaduras y de ideales.

La noción de cortadura, o sección, expuesta en su trabajo Stetigkeit und irralionale Zahlen (1ª ed., 1872, 24 pág.), se ha hecho clásica en la exposición de la teoría de los números irracionales, pues presenta la gran ventaja de no tener que utilizar la noción de límite en momento poco oportuno, y a pesar de las teorías que acerca del mismo tema expusieron Meray-Cantor y Weierstrass, la teoría de Dedekind suele preferirse en la enseñanza elemental.